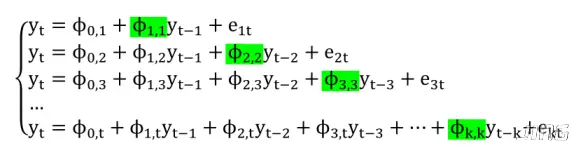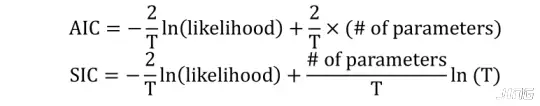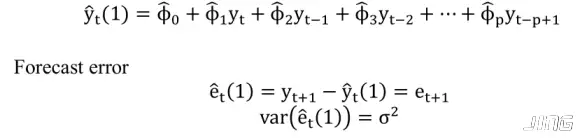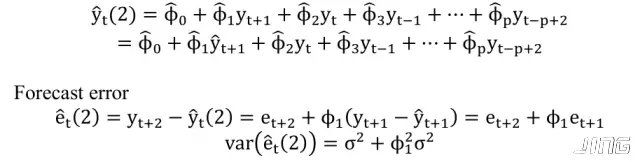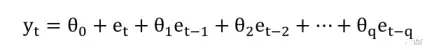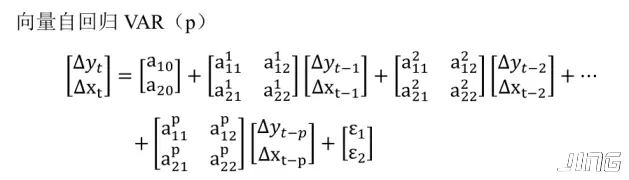时间序列基础

Time Series Models , 整体是有关未来的预测, 可能是由 Y 自身出发进行

plot 先观察变量的变化趋势

数据处理

滞后 (Lags 即是上一期的数据) L.Y
一阶差分 (First difference) D.Y
$\Delta Y_t=Y_t-Y_{t-1}\Rightarrow \Delta Y_t=Y_t-L.Y_{t}=(1-L)Y_t$
$\Delta^2 Y_t==(1-L)^2 Y_t$
$\Delta^3 Y_t==(1-L)^3 Y_t$
自然对数与增长率
取对数可将指数增长变成线性变化
应对存在的异方差问题
$Growth \ Rate =\frac{Y_t-Y_{t-1}}{Y_{t-1}}=\frac{\Delta Y_t}{Y_{t-1}} \approx \Delta ln(Y_t)$
$\Delta ln(Y_t)=ln(Y_t)-ln(Y_{t-1})$
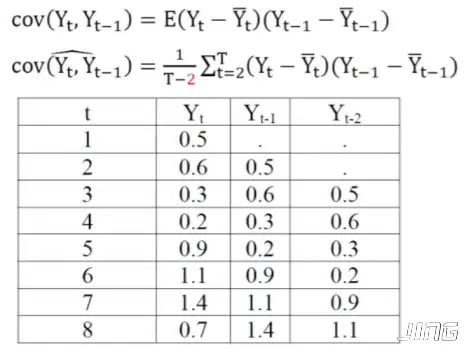
自协方差
$Cov(Y_t,Y_{t-1})$
自相关系数
$\rho \Rightarrow (X \ and \ Y)$
$\widehat{\rho} \Rightarrow (\widehat{X} \ and \ Y)$
$j^{th}autocorrelation=\rho_j=\frac{cov(Y_t,Y_{t-1})} {\sqrt{var(Y_t)var(Y_{t-j} ) } }$
自协方差及自相关均可以在 stata 做时间序列图
1
2
3
pwcorr y1 L2.ya,sig //y1 与滞后一阶
corrgram y1,lag(20) //y1 与滞后 20 阶之前的自相关系数
ac y1 // 作自相关系数图 & 置信区间

平稳性及其检验

过去的变化及波动应该处于合理的区间, 以保障预测存在合理性；

严平稳性 - $y_t$
$\{y_1,y_2,...,y_t\}$ 的联合概率分布与 $\{y_{1+k},y_{2+k},...,y_{t+k}\}$ 的联合概率分布相同
弱平稳性（常用）
$y_t$ 的均值、方差不随时间变化, 协方差仅与观测值之间的距离而与所处的时间点无关
$E(y_t)=\mu$
$var(y_t)=E(y_t-\mu)^2=\sigma^2$
$cov(y_t,y_{t+k})=\gamma_{k}=E[(y_t-\mu)(y_{t+k}-\mu)]=E[(y_{t+m}-\mu)(y_{t+m+k}-\mu)]$
非平稳时, 期望值是依赖时间变化的

常见非平稳随机过程 (stochastic processes)

无漂浮随机游走 (Random Walk without Drift)
$Y_t=Y_{t-1}+e_t$
其中 $e_t$ 是均值为 0, 方差为 $\sigma^2$ 的白噪声 (shock)
$Y_t=Y_0+\sum e_t$
then:
$E(Y_t)=E(Y_0+\sum e_t)=Y_0$
$var(Y_t)=t\sigma ^2$
随时间的增加, 方差会增大；
有漂浮随机游走 (Random Walk with Drift)
$y_t=\delta+y_{t-1}+e_t$ (漂浮项 $\delta$ , 使时间序列有时间趋势——非平稳)

伪回归现象 (spurious regression)

时间序列不平稳时, 产生伪回归现象；
$Y_t=Y_0+\sum e_1t$
$X_t=X_0+\sum e_2t$
$e_1t$ 与 $e_2t$ 弱相关关系, 由此产生的两个随机游走时间序列应同样没有相关关系, 但回归测试后发现存在显著相关关系；
对两个序列做差分, 可能会使序列变得平稳；
回归之前需要先检验, 如果检验不平稳, 需要处理为平稳序列；

平稳性检验

避免伪回归现象；
判断方法：
散点图判断平稳性（看均值或者离散程度）；
样本自相关函数判断平稳性：
总体自相关函数(autocorrelation function, ACF)
$\rho_k=\frac{\gamma_k} {\gamma_0}=\frac{cov(y_t,y_{t+k} ) } {var(y_t) }$
样本 ACF
$\widehat {\rho_k} = \frac{\widehat {\gamma} _ k } {\widehat {\gamma} _ 0 } = \frac {\sum(y _ t - \overline {y} ) (y _ {t+k} - \overline{y} ) } {\sum(y_t - \overline {y} ) ^ 2 }$
白噪声的 $ACF=0$ , 是没有信息可以提取的平稳序列；
非平稳序列的 ACF 衰减比较慢；
White Noise (i.i.d- independent and identically distributed)
Gaussian white noise: 服从 0 均值, $\sigma^2$ 方差的正态分布;
All the ACFS are zeros;
Test:
Portmanteau (Q)Statistic： $Q^*=T\sum^{m}_{l=1}\widehat{\rho}_l^2$
1
wntestq yt,lags(50) // 选择 50 以内的全部滞后期, 即选择 50 个 ACF 加总
非平稳时间序列 ACF 特征：当 k 增大时, 衰减比较慢；
平稳时间序列 ACF 特征：当 k 增大时, 衰减比较快；
单位根 (unit root)
$y_t=\rho y_{t-1}+e_t$
$y_t-\rho y_{t-1}=e_t$
$y_t-\rho L y_t=e_t$
$(1-\rho L)y_t=e_t$
$\Rightarrow 1-\rho z=0$
$z=\frac{1}{\rho}>1$ 为平稳序列
$\rho=1$ 则该过程为无漂移随机游走随机过程, 该过程非平稳, 称该过程具有单位根；可以做一次差分使序列变得平稳；（一个单位根）
$|\rho|<1$ 时, 可以证明 $y_t$ 是平稳的；
若 $y_t=2y_{t-1}-y_{t-2}+e_t$ 可得 $z_1=1, z_2=1$ 存在两个单位根, 做两次差分, 变得平稳；
Dickey-Fuller 单位根检验
$y_t=\rho y_{t-1}+e_t$
两边同时减去 $y_{t-1}$
then: $y_t-y_{t-1}=(\rho-1)y_{t-1}+e_t$ 即 $\Delta y_t=\delta y_{t-1}+e_t$
检验原假设： $H_0:\delta=0$
1
dfuller dlny //test for unit root
Augmented Dickey-Fuller (ADF) test
$\Delta y_t = \delta y_{t-1} + \sum^{L} _ {j=1} \lambda_j \Delta y_{t-j}+e_t$
$\Delta y_t=\alpha+\delta y_{t-1} + \sum^{L} _ {j=1} \lambda_j \Delta y_{t-j}+e_t$
$\Delta y_t=\alpha+\beta t+\delta y_{t-1}+\sum^{L} _ {j=1} \lambda_j \Delta y_{t-j}+e_t$
带有时间趋势项的非平稳序列, 可以通过去除趋势项使其变的平稳；

AR 模型

时间序列分析是短期预测方法, 时间序列模型不是不同变量间的“因果”关系为基础, 而是寻找时间序列自身的变化规律；
Autoregression Integrated Moving Average model （or Box-Jenkins 方法）
先将非平稳序列处理平稳, 再建模；
依据变量自身的变化规律, 利用外推机制描述时间序列的变化；
AR 模型 (Autoregression Model)
一阶自回归—AR(1)
$y_t=\phi_0+\phi_1 y_{t-1}+e_t$
p 阶自回归—AR(p)
$y_t=\phi_0+\phi_1 y_{t-1}+\phi_2 y_{t-2}+\phi_3 y_{t-3}+...+\phi_p y_{t-p}+e_t$
AR 模型识别
(1) 利用 ACF (Autocorrelation Function) 和 PACF (Partial Autocorrelation Function)
ACF 自相关函数 $\rho_k=\frac{\gamma_k}{\gamma_0}=\frac{cov(y_t,y_{t+k})}{var(y_t)}$
PACF：描述 $y_t$ 与 $y_{t-k}$ 之间的条件相关性, 即在消除中间变量 $y_{t-1},...,y_{t-k+1}$ 带来的间接相关性后, $y_t$ 与 $y_{t+k}$ 之间的直接相关性；
PACF 由 Yule-Walker 方程求出；

(2) 利用 AIC、SIC 等信息准则
AR 模型估计：
OLS
MLE
AR 模型预测
(1) 1-step ahead Forecasting

(2) 2-step ahead forecasting

(3) multistep ahead Forecasting

MA (moving average)模型

模型设定
MA(1)
MA(q)
模型识别
$AR(\infty) \rightarrow MA(1)$
PACF: decay
ACF: cut off
模型估计
MLE
模型预测
1-step ahead
2-step ahead
3-step ahead

ARMA 模型

结合 AR 和 MA 模型

ARIMA(p, d, q)模型建模

对原序列进行平稳性检验, 如果不满足平稳性的条件, 可以通过差分变
换或者其他变换（如先取对数然后再差分）将该序列变为平稳序列；
对平稳序列计算 ACF 和 PACF, 初步确定 ARMA 模型的阶数 p 和 q, 并
在初始估计中选择尽可能较少的参数；
估计 ARMA 模型的参数, 借助 t 统计量初步判断参数的显著性, 尽可能
剔除不显著的参数, 保持模型的结构精简；
对估计的 ARMA 模型的扰动项进行检验, 看其是否为白噪声序列；
当有几个较为相似的 ARMA 模型可供选择时, 可以通过 AIC 或 SIC 等
标准来选择最优模型。

协整

不平稳的变量, 不能使用经典回归模型, 否则会出现伪回归问题；
非平稳 → 差分转换成平稳 → 适合描述短期状态或非均衡状态− 长期均衡状态应该使用变量本身（level data）
如果在一个回归中涉及的两个或多个时间序列“一起漂移”或“同步”, 则可能没有伪回归问题。
协整：
协整检验：
两变量 Engle-Granger 检验

误差修正

ECM 模型

Granger 因果关系检验

一般在 VAR 模型框架下进行
检验假设

ARCH 和 GARCH

金融时间序列
原数据是随机游走（random walk）过程（非平稳的）；
一阶差分后是平稳的, 但是表现为剧烈波动性, 这种波动性表现在两个方面：
— 波动性随时间而变化；波动性聚集现象（volatility clustering）
自回归条件异方差模型 (Autoregressive Conditional Heteroscedasticity , ARCH)
广义自回归条件异方差模型 (Generalized Autoregressive Conditional Heteroscedasticity, GARCH)