展开式与矩阵形式的方程及模型设定
经典假设——5 条E ( μ i ) = 0 E(\mu_i)=0 E ( μ i ) = 0 E ( μ ′ μ ) = σ 2 I E(\mu'\mu)=\sigma^2I E ( μ ′ μ ) = σ 2 I μ ∼ N ( 0 , σ 2 I ) \mu\thicksim N(0,\sigma^2I) μ ∼ N ( 0 , σ 2 I )
OLS 估计
极大似然估计
MM 矩估计β ^ = ( X ′ X ) − 1 X ′ Y \widehat{\beta}=(X'X)^{-1}X'Y β = ( X ′ X ) − 1 X ′ Y β ^ = ( x ′ x ) − 1 x ′ Y \widehat{\beta}=(x'x)^{-1}x'Y β = ( x ′ x ) − 1 x ′ Y
满足经典假设的估计量性质：c o v ( β ^ ) = σ 2 ( X ′ X ) − 1 cov(\widehat{\beta})=\sigma^2(X'X)^{-1} c o v ( β ) = σ 2 ( X ′ X ) − 1
σ ^ 2 = e ′ e n − k − 1 \widehat{\sigma}^2=\frac{e'e} {n-k-1} σ 2 = n − k − 1 e ′ e
拟合优度：R 2 = E S S T S S R^2=\frac{ESS}{TSS} R 2 = T S S E S S a d j − R 2 = 1 − ( 1 − R 2 ) ∗ n − 1 n − k − 1 adj-R^2=1-(1-R^2)*\frac{n-1}{n-k-1} a d j − R 2 = 1 − ( 1 − R 2 ) ∗ n − k − 1 n − 1 l n e ′ e n + 2 ( k + 1 ) n ln\frac{e'e}{n}+\frac{2(k+1)}{n} l n n e ′ e + n 2 ( k + 1 ) l n e ′ e n + k n l n n ln\frac{e'e}{n}+\frac{k}{n}lnn l n n e ′ e + n k l n n
回归方程显著——F 统计量F = E S S / k R S S / n − k − 1 = R 2 1 − R 2 × n − k − 1 k ∼ F ( k , n − k − 1 ) F=\frac{ESS/k}{RSS/n-k-1}=\frac{R^2}{1-R^2}\times\frac{n-k-1}{k}\thicksim F(k,n-k-1) F = R S S / n − k − 1 E S S / k = 1 − R 2 R 2 × k n − k − 1 ∼ F ( k , n − k − 1 )
受约束回归 / 解释变量数量是否变动：F = R S S R − R S S U / ( k U − k R ) R S S U / ( n − k − 1 ) ∼ F ( k U − k R , n − k − 1 ) F=\frac{RSS_R-RSS_U/(k_U-k_R)}{RSS_U/(n-k-1)}\thicksim F(k_U-k_R,n-k-1) F = R S S U / ( n − k − 1 ) R S S R − R S S U / ( k U − k R ) ∼ F ( k U − k R , n − k − 1 )
变量显著性检验——t 统计量t = β ^ − β s e ( β ^ ) ∼ t ( n − 2 ) t=\frac{\widehat{\beta}-\beta}{se(\widehat{\beta}) }\thicksim t(n-2) t = s e ( β ) β − β ∼ t ( n − 2 )
参数置信区间：( β ^ − t α 2 × s e ( β ^ ) , β ^ + t α 2 × s e ( β ^ ) ) (\widehat{\beta}-t_{\frac{\alpha} {2} }\times se(\widehat{\beta} ),\widehat{\beta}+t_{\frac{\alpha} {2} }\times se(\widehat{\beta} ) ) ( β − t 2 α × s e ( β ) , β + t 2 α × s e ( β ) )
s e ( β ^ ) = σ ^ C i i se(\widehat{\beta} )=\widehat{\sigma} C_{ii} s e ( β ) = σ C i i
E ( Y 0 ) E(Y_0) E ( Y 0 ) Y 0 ^ − t α 2 × s e ( Y 0 ^ ) , Y 0 ^ + t α 2 × s e ( Y 0 ^ ) \widehat{Y_0}-t_{\frac{\alpha}{2}}\times se(\widehat{Y_0}),\widehat{Y_0}+t_{\frac{\alpha}{2}}\times se(\widehat{Y_0}) Y 0 − t 2 α × s e ( Y 0 ) , Y 0 + t 2 α × s e ( Y 0 )
s e ( Y 0 ^ ) = σ ^ X 0 ( X ′ X ) − 1 X 0 ′ se(\widehat{Y_0})=\widehat{\sigma}\sqrt{X_0(X'X)^{-1}X_0'} s e ( Y 0 ) = σ X 0 ( X ′ X ) − 1 X 0 ′
Y 0 Y_0 Y 0 e 0 = Y 0 − Y 0 ^ e_0=Y_0-\widehat{Y_0} e 0 = Y 0 − Y 0
[ Y 0 ^ − t α 2 × s e ( e 0 ) , Y 0 ^ + t α 2 × s e ( e 0 ) ] [\widehat{Y_0}-t_{\frac{\alpha}{2}}\times se(e_0),\widehat{Y_0}+t_{\frac{\alpha}{2}}\times se(e_0)] [ Y 0 − t 2 α × s e ( e 0 ) , Y 0 + t 2 α × s e ( e 0 ) ]
s e ( e 0 ) = σ ^ 1 + X 0 ( X ′ X ) − 1 X 0 ′ se(e_0)=\widehat{\sigma}\sqrt{1+X_0(X'X)^{-1}X_0'} s e ( e 0 ) = σ 1 + X 0 ( X ′ X ) − 1 X 0 ′
c 1 x i 1 + c 2 x i 2 + . . . + c k x i k = 0 c_1 x_{i1}+c_2 x_{i2}+...+c_k x_{ik}=0 c 1 x i 1 + c 2 x i 2 + . . . + c k x i k = 0 c i c_i c i
c 1 x i 1 + c 2 x i 2 + . . . + c k x i k + v i = 0 c_1 x_{i1}+c_2 x_{i2}+...+c_k x_{ik}+v_i=0 c 1 x i 1 + c 2 x i 2 + . . . + c k x i k + v i = 0 c i c_i c i v i v_i v i
Rank ( X ) < k + 1 \text{Rank}(X)<k+1 Rank ( X ) < k + 1
产生原因：
多重共线性后果( X ′ X ) − 1 (X'X)^{-1} ( X ′ X ) − 1 C o v ( β ^ ) = σ 2 ( X ′ X ) − 1 Cov(\widehat{\beta})=\sigma^2(X'X)^{-1} C o v ( β ) = σ 2 ( X ′ X ) − 1 r 2 = ∑ x 1 i x 2 i ∑ x 1 i ∑ x 2 i r^2=\frac{\sum x_{1i} x_{2i}}{\sum x_{1i} \sum x_{2i}} r 2 = ∑ x 1 i ∑ x 2 i ∑ x 1 i x 2 i
r 2 = 0 r^2=0 r 2 = 0 v a r ( β ^ ) = σ 2 ∑ x 1 2 var(\widehat{\beta})=\frac{\sigma^2}{\sum x_1^2} v a r ( β ) = ∑ x 1 2 σ 2
0 < r 2 < 1 0<r^2<1 0 < r 2 < 1 v a r ( β ^ ) = σ 2 ∑ x 1 2 × 1 1 − r 2 > σ 2 ∑ x 1 2 var(\widehat{\beta})=\frac{\sigma^2}{\sum x_1^2} \times \frac{1}{1-r^2}>\frac{\sigma^2}{\sum x_1^2} v a r ( β ) = ∑ x 1 2 σ 2 × 1 − r 2 1 > ∑ x 1 2 σ 2 1 1 − r 2 \frac{1}{1-r^2} 1 − r 2 1
r 2 = 1 r^2=1 r 2 = 1 v a r ( β ^ ) = ∞ var(\widehat{\beta})=\infty v a r ( β ) = ∞
估计量不具有经济含义
检验多重共线性问题r 2 r^2 r 2 R 2 R^2 R 2 F F F t t t 判定系数法 ：对每一解释变量以其他变量作为解释变量作辅助回归,X j i = α 1 X 1 i + α 2 X 2 i + . . . + α k X k i X_{ji}=\alpha_1 X_{1i}+\alpha_2 X_{2i}+...+\alpha_k X_{ki} X j i = α 1 X 1 i + α 2 X 2 i + . . . + α k X k i R j 2 R^2_j R j 2 F = R j 2 / ( k − 1 ) ( 1 − R j 2 ) / ( n − k ) ∼ F ( k − 1 , n − k ) F=\frac{R^2_j/(k-1)}{(1-R^2_j)/(n-k)}\thicksim F(k-1,n-k) F = ( 1 − R j 2 ) / ( n − k ) R j 2 / ( k − 1 ) ∼ F ( k − 1 , n − k ) 排除变量法 ：比较排除一个解释变量与加入改解释变量的R 2 R^2 R 2 逐步回归法 ：逐步加入解释变量, 观察R 2 R^2 R 2
克服多重共线性：以引入偏误为代价, 减小参数估计量的方差
β ^ = ( X ′ X + D ) − 1 X ′ Y \widehat{\beta}=(X'X+D)^{-1}X'Y β = ( X ′ X + D ) − 1 X ′ Y
v a r ( μ i ) = σ i 2 var(\mu_i)=\sigma^2_i v a r ( μ i ) = σ i 2 σ i 2 = \sigma^2_i= σ i 2 = ≠ f ( X i ) \neq f(X_i) = f ( X i ) σ i 2 = f ( X i ) \sigma_i^2=f(X_i) σ i 2 = f ( X i ) σ i 2 = f ( X i ) \sigma^2_i=f(X_i) σ i 2 = f ( X i ) σ \sigma σ X X X
异方差的后果：E ( μ ′ μ ) = σ 2 I E(\mu'\mu)=\sigma^2I E ( μ ′ μ ) = σ 2 I σ 2 \sigma^2 σ 2 s e ( β ^ ) se(\widehat{\beta}) s e ( β ) s e ( β ^ ) se(\widehat{\beta}) s e ( β )
检验异方差：
v a r μ i = E ( μ i 2 ) ≈ e i ~ 2 var{\mu_i}=E(\mu_i^2)\approx \widetilde{e_i}^2 v a r μ i = E ( μ i 2 ) ≈ e i 2
e i ~ = Y i − ( Y i ^ ) o l s \widetilde{e_i}=Y_i-(\widehat{Y_i})_{ols} e i = Y i − ( Y i ) o l s
图示法 ：
X-e ~ 2 \widetilde{e}^2 e 2 布罗施 - 帕甘 (B-P) 检验 ：
e ~ 2 = δ 0 + δ 1 X i 1 + δ 2 X i 2 + . . . + δ k X i k + ε i \widetilde{e}^2=\delta_0+\delta_1X_{i1}+\delta_2X_{i2}+...+\delta_kX_{ik}+\varepsilon_i e 2 = δ 0 + δ 1 X i 1 + δ 2 X i 2 + . . . + δ k X i k + ε i
检验联合假设H 0 : δ 0 = δ 1 = δ 2 = . . . = δ k = 0 H_0:\delta_0=\delta_1=\delta_2=...=\delta_k=0 H 0 : δ 0 = δ 1 = δ 2 = . . . = δ k = 0
有R 2 R^2 R 2
F = R 2 / k ( 1 − R 2 ) / ( n − k − 1 ) ∼ F ( k , n − k − 1 ) F=\frac{R^2/k}{(1-R^2)/(n-k-1)}\thicksim F(k,n-k-1) F = ( 1 − R 2 ) / ( n − k − 1 ) R 2 / k ∼ F ( k , n − k − 1 )
L M = n ⋅ R 2 ∼ X 2 ( K ) LM=n·R^2\thicksim X^2(K) L M = n ⋅ R 2 ∼ X 2 ( K )
怀特 (White) 检验 ：Y i = β 0 + β 1 X i 1 + β 2 X i 2 + μ i Y_i=\beta_0+\beta_1X_{i1}+\beta_2X_{i2}+\mu_i Y i = β 0 + β 1 X i 1 + β 2 X i 2 + μ i e i ~ 2 = Y i − Y i ^ \widetilde{e_i}^2=Y_i-\widehat{Y_i} e i 2 = Y i − Y i e i ~ 2 = α 0 + α 1 X i 1 + α 2 X i 2 + α 3 X i 1 2 + α 4 X i 2 2 + α 5 X i 1 X i 2 + ε i \widetilde{e_i}^2=\alpha_0+\alpha_1X_{i1}+\alpha_2X_{i2}+\alpha_3X_{i1}^2+\alpha_4X_{i2}^2+\alpha_5X_{i1}X_{i2}+\varepsilon_i e i 2 = α 0 + α 1 X i 1 + α 2 X i 2 + α 3 X i 1 2 + α 4 X i 2 2 + α 5 X i 1 X i 2 + ε i n R 2 ∼ X 2 ( h ) nR^2\sim X^2(h) n R 2 ∼ X 2 ( h )
异方差的修正：加权最小二乘法
∑ W i e i 2 \sum W_ie_i^2 ∑ W i e i 2 e i 2 e_i^2 e i 2 e i 2 e_i^2 e i 2
v a r ( μ i ) = E ( μ i 2 ) = f ( X i j ) σ 2 var(\mu_i)=E(\mu_i^2)=f(X_{ij})\sigma^2 v a r ( μ i ) = E ( μ i 2 ) = f ( X i j ) σ 2
1 f ( X i j ) Y i = 1 f ( X i j ) β 0 + 1 f ( X i j ) β 1 X i 1 + 1 f ( X i j ) β 2 X i 2 + . . . + 1 f ( X i j ) β k X i k + 1 f ( X i j ) μ i \frac{1}{f(X_{ij})}Y_i=\frac{1}{f(X_{ij})}\beta_0+\frac{1}{f(X_{ij})}\beta_1X_{i1}+\frac{1}{f(X_{ij})}\beta_2X_{i2}+...+\frac{1}{f(X_{ij})}\beta_kX_{ik}+\frac{1}{f(X_{ij})}\mu_i f ( X i j ) 1 Y i = f ( X i j ) 1 β 0 + f ( X i j ) 1 β 1 X i 1 + f ( X i j ) 1 β 2 X i 2 + . . . + f ( X i j ) 1 β k X i k + f ( X i j ) 1 μ i
⇒ v a r ( μ i ∗ ) = 1 f ( X i j ) E ( μ i 2 ) = σ 2 \Rightarrow var(\mu_i^*)=\frac{1}{f(X_{ij})}E(\mu_i^2)=\sigma^2 ⇒ v a r ( μ i ∗ ) = f ( X i j ) 1 E ( μ i 2 ) = σ 2
⇒ β ^ = ( X ∗ ′ X ∗ ) − 1 X ∗ ′ Y ∗ \Rightarrow \widehat {\beta} = (X ^ { * '} X ^ * ) ^ {-1} X ^ {* '} Y ^ * ⇒ β = ( X ∗ ′ X ∗ ) − 1 X ∗ ′ Y ∗
方差μ \mu μ X X X
异方差稳健标准误法
内生解释变量：
内生解释变量产生原因：
内生解释变量问题的后果：
工具变量法：β 1 ^ = ∑ z i y i ∑ z i x i \widehat{\beta_1}=\frac{\sum z_i y_i}{\sum z_i x_i} β 1 = ∑ z i x i ∑ z i y i β ^ = ( Z ′ X ) − 1 Z ′ Y \widehat{\beta}=(Z'X)^{-1}Z'Y β = ( Z ′ X ) − 1 Z ′ Y
三种估计方法：IV ：X ^ i = α ^ 0 + α ^ 1 Z i \widehat{X}_i=\widehat{\alpha}_0+\widehat{\alpha}_1Z_i X i = α 0 + α 1 Z i
由第一步得到的X ^ i \widehat{X}_i X i Y ^ i = β ~ 0 + β ~ 1 X ^ i \widehat{Y}_i=\widetilde{\beta}_0+\widetilde{\beta}_1 \widehat{X}_i Y i = β 0 + β 1 X i
得到β ^ 1 = ∑ z i y i ∑ z i x i \widehat{\beta}_1=\frac{\sum z_i y_i}{\sum z_i x_i} β 1 = ∑ z i x i ∑ z i y i
2SLS : 一个内生解释变量有多个工具变量Y i = β 0 + β 1 X i + β 2 Z i + μ i Y_i=\beta_0+\beta_1X_i+\beta_2Z_i+\mu_i Y i = β 0 + β 1 X i + β 2 Z i + μ i
第一阶段, 内生解释变量 X 关于工具变量Z 1 Z_1 Z 1 Z 2 Z_2 Z 2 Z Z Z
X ^ i = α ^ 0 + α ^ 1 Z i 1 + α ^ 2 Z i 2 + α ^ 3 Z i \widehat {X} _ i = \widehat {\alpha} _0 + \widehat {\alpha} _1 Z_ {i1} + \widehat {\alpha} _2 Z_{i2} + \widehat {\alpha} _3 Z _ {i} X i = α 0 + α 1 Z i 1 + α 2 Z i 2 + α 3 Z i
第二阶段, 以第一阶段的X ^ i \widehat{X}_i X i X i X_i X i
Y i = β 0 + β 1 X ^ i + β 2 Z i + μ i Y_i=\beta_0+\beta_1\widehat{X}_i+\beta_2Z_i+\mu_i Y i = β 0 + β 1 X i + β 2 Z i + μ i
得到一致估计量；
GMM 广义矩估计 ：一个内生解释变量有多个工具变量
内生性检验：豪斯曼 (Hausman) 检验 ：Z 1 Z_1 Z 1 Z 2 Z_2 Z 2
X i = α 0 + α 1 Z i 1 + α 2 Z i 2 + v i X_i=\alpha_0+\alpha_1Z_{i1}+\alpha_2Z_{i2}+v_i X i = α 0 + α 1 Z i 1 + α 2 Z i 2 + v i
第二步：将残差加入原模型, 再做 OLS 估计：
Y i = β 0 + β 1 X i + β 2 Z i 1 + δ V ^ i + ε i Y_i=\beta_0+\beta_1X_i+\beta_2Z_{i1}+\delta \widehat{V}_i+\varepsilon_i Y i = β 0 + β 1 X i + β 2 Z i 1 + δ V i + ε i
如果V ^ \widehat{V} V μ \mu μ Z 1 , Z 2 Z_1,Z_2 Z 1 , Z 2 μ \mu μ μ \mu μ
不拒绝δ = 0 \delta=0 δ = 0
若有多个内生变量, 则逐个与外生变量做 OLS, 并将得到的残差都引入原模型；
过度识别约束检验：
随机项之间存在相关性:c o v ( μ i , μ j ) = E ( μ i , μ j ) ≠ 0 cov(\mu_i,\mu_j)=E(\mu_i,\mu_j)\neq 0 c o v ( μ i , μ j ) = E ( μ i , μ j ) = 0 v a r ( μ ) = E ( μ μ ′ ) = σ 2 Ω ≠ σ 2 I var(\mu)=E(\mu \mu')=\sigma^2\Omega\neq\sigma^2I v a r ( μ ) = E ( μ μ ′ ) = σ 2 Ω = σ 2 I
仅存在c o v ( μ t , μ t + 1 ) ≠ 0 cov(\mu_t,\mu_{t+1})\neq0 c o v ( μ t , μ t + 1 ) = 0 μ t + 1 = ρ μ t + ε t \mu_{t+1}=\rho \mu_t+\varepsilon_t μ t + 1 = ρ μ t + ε t ρ \rho ρ
白噪声 ：
ε t \varepsilon_t ε t
E ( ε t ) = 0 E(\varepsilon_t)=0 E ( ε t ) = 0 v a r ( ε t ) = σ 2 var(\varepsilon_t)=\sigma^2 v a r ( ε t ) = σ 2 c o v ( ε i , ε i − s ) = 0 cov(\varepsilon_i,\varepsilon_{i-s})=0 c o v ( ε i , ε i − s ) = 0
产生序列相关的原因：
序列相关的后果：参数估计量非有效 E ( μ ′ μ ) ≠ σ 2 I E(\mu'\mu)\neq\sigma^2I E ( μ ′ μ ) = σ 2 I 变量显著性检验失去意义 ：显著性检验同样建立在随机误差项同方差及相互独立的基础上, 存在序列相关时, 参数的方差估计存在偏误, t 统计量存在偏误；模型预测失效 ：异方差, 参数估计量方差的估计量存在偏误, 预测区间精度降低；
序列相关检验：e t ~ = Y t − Y t ^ \widetilde{e_t}=Y_t-\widehat{Y_t} e t = Y t − Y t 图示法 ——e t ~ − t \widetilde{e_t}-t e t − t 回归检验法 ：e t ~ \widetilde{e_t} e t e ~ t − 1 \widetilde{e} _ {t-1} e t − 1 e ~ t − 2 \widetilde{e} _ {t-2} e t − 2 e ~ t 2 \widetilde{e} _t ^ 2 e t 2
利于确定序列相关的形式, 适用于任何类型的序列相关问题检验；杜宾 - 瓦森 D.W. 检验法 ：检验序列自相关；
随机误差项μ t \mu_t μ t μ t = ρ μ t − 1 + ε t \mu_t=\rho\mu_{t-1}+\varepsilon_t μ t = ρ μ t − 1 + ε t
回归模型中不含有被解释变量滞后项
回归具有截距项
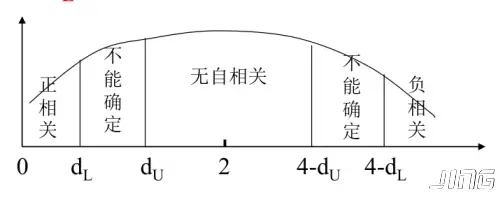
构造D . W . D.W. D . W . = ∑ t = 2 n ( e ~ t − e ~ t − 1 ) ∑ t = 1 n e ~ t 2 =\frac{\sum_{t=2} ^ n (\widetilde{e} _ t-\widetilde{e} _ {t-1})}{\sum_{t=1} ^n \widetilde{e} _ t ^ 2} = ∑ t = 1 n e t 2 ∑ t = 2 n ( e t − e t − 1 )
临界值的下限d L d_L d L d U d_U d U
给定显著水平α \alpha α
比较、判断：
0 < D W < d L 0<DW<d_L 0 < D W < d L
d L < D W < d U d_L<DW<d_U d L < D W < d U
d U < D W < 4 − d U d_U<DW<4-d_U d U < D W < 4 − d U
4 − d u < D W < 4 − d L 4-d_u<DW<4-d_L 4 − d u < D W < 4 − d L
4 − d L < D W < 4 4-d_L<DW<4 4 − d L < D W < 4
D . W . ≈ 2 ( 1 − ρ ) D.W.\approx 2(1-\rho) D . W . ≈ 2 ( 1 − ρ )
一阶自回归中, 估计ρ = ∑ t = 2 n e ~ t e ~ t − 1 ∑ t = 2 n e ~ t 2 \rho= \frac {\sum_ { t=2} ^ n \widetilde {e} _ t \widetilde {e} _ {t - 1} } {\sum_ { t = 2} ^ n \widetilde {e} _ t ^ 2} ρ = ∑ t = 2 n e t 2 ∑ t = 2 n e t e t − 1
完全一阶正相关,ρ = 1 \rho=1 ρ = 1 D . W . ≈ 0 D.W.\approx 0 D . W . ≈ 0
完全一阶负相关,ρ = − 1 \rho=-1 ρ = − 1 D . W . ≈ 4 D.W.\approx 4 D . W . ≈ 4
完全一阶不相关,ρ = 0 \rho=0 ρ = 0 D . W . ≈ 2 D.W.\approx 2 D . W . ≈ 2
拉格朗日乘数检验 : 适合高阶序列相关及模型中包含被解释变量滞后项的情形（BG 检验 ）Y t = β 0 + β 1 X t 1 + β 2 X t 2 + . . . + β k X t k + μ t Y_t=\beta_0+\beta_1X_{t1}+\beta_2X_{t2}+...+\beta_kX_{tk}+\mu_t Y t = β 0 + β 1 X t 1 + β 2 X t 2 + . . . + β k X t k + μ t
怀疑μ t \mu_t μ t p p p
μ t = ρ 1 μ t − 1 + ρ 2 μ t − 2 + . . . + ρ p μ t − p + ε t \mu_t=\rho_1\mu_{t-1}+\rho_2\mu_{t-2}+...+\rho_p\mu_{t-p}+\varepsilon_t μ t = ρ 1 μ t − 1 + ρ 2 μ t − 2 + . . . + ρ p μ t − p + ε t
BG 检验：构造受约束回归方程:
Y t = β 0 + β 1 X t 1 + β 2 X t 2 + . . . + β k X t k + ρ 1 μ t − 1 + ρ 2 μ t − 2 + . . . + ρ p μ t − p + ε t Y_t=\beta_0+\beta_1X_{t1}+\beta_2X_{t2}+...+\beta_kX_{tk}+\rho_1\mu_{t-1}+\rho_2\mu_{t-2}+...+\rho_p\mu_{t-p}+\varepsilon_t Y t = β 0 + β 1 X t 1 + β 2 X t 2 + . . . + β k X t k + ρ 1 μ t − 1 + ρ 2 μ t − 2 + . . . + ρ p μ t − p + ε t
约束条件H 0 : ρ 1 = ρ 2 = . . . = ρ p = 0 H_0:\rho_1=\rho_2=...=\rho_p=0 H 0 : ρ 1 = ρ 2 = . . . = ρ p = 0
计算残差序列e ~ t \widetilde{e}_t e t
构造辅助回归：
e ~ t = β 0 + β 1 X t 1 + β 2 X t 2 + . . . + β k X t k + ρ 1 e ~ t − 1 + ρ 2 e ~ t − 2 + . . . + ρ p e ~ t − p + ε t \widetilde {e} _ t = \beta _ 0 + \beta _ 1 X _ {t 1} + \beta _ 2 X _ {t 2} + ... +\beta _ k X _ {tk} +\rho _ 1 \widetilde {e} _ {t - 1} + \rho _ 2 \widetilde {e} _ {t -2} +... + \rho_p \widetilde {e} _ {t - p} + \varepsilon _ t e t = β 0 + β 1 X t 1 + β 2 X t 2 + . . . + β k X t k + ρ 1 e t − 1 + ρ 2 e t − 2 + . . . + ρ p e t − p + ε t
计算辅助回归的R 2 R^2 R 2
约束为真时, 大样本下L M = n ⋅ R 2 ∼ χ 2 ( p ) LM=n·R^2\thicksim \chi^2(p) L M = n ⋅ R 2 ∼ χ 2 ( p )
给定显著水平α \alpha α χ α 2 ( p ) \chi_\alpha^2(p) χ α 2 ( p ) L M LM L M
序列相关补救:广义最小二乘法(GLS) ：C o v ( μ μ ′ ) = E ( μ μ ′ ) = σ 2 Ω Cov(\mu \mu')=E(\mu \mu')=\sigma^2\Omega C o v ( μ μ ′ ) = E ( μ μ ′ ) = σ 2 Ω
存在可逆矩阵 D 使Ω = D ′ D \Omega=D'D Ω = D ′ D
变换原模型：D − 1 Y = D − 1 X β + D − 1 μ D^{-1}Y=D^{-1}X\beta+D^{-1}\mu D − 1 Y = D − 1 X β + D − 1 μ
E ( μ ∗ μ ∗ ′ ) = σ 2 I E(\mu_* \mu_*')=\sigma^2I E ( μ ∗ μ ∗ ′ ) = σ 2 I
OLS 估计：β ^ ∗ = ( X ′ Ω − 1 X ) − 1 X ′ Ω − 1 Y \widehat{\beta}_*=(X'\Omega^{-1}X)^{-1}X'\Omega^{-1}Y β ∗ = ( X ′ Ω − 1 X ) − 1 X ′ Ω − 1 Y
广义差分法 ：将模型变化为不存在序列相关的差分模型, 再 OLS 估计：Y t = β 0 + β 1 X t 1 + β 2 X t 2 + . . . + β k X t k + μ t Y_t=\beta_0+\beta_1X_{t1}+\beta_2X_{t2}+...+\beta_kX_{tk}+\mu_t Y t = β 0 + β 1 X t 1 + β 2 X t 2 + . . . + β k X t k + μ t
怀疑μ t \mu_t μ t
μ t = ρ 1 μ t − 1 + ρ 2 μ t − 2 + . . . + ρ p μ t − p + ε t \mu_t=\rho_1\mu_{t-1}+\rho_2\mu_{t-2}+...+\rho_p\mu_{t-p}+\varepsilon_t μ t = ρ 1 μ t − 1 + ρ 2 μ t − 2 + . . . + ρ p μ t − p + ε t
差分变化：Y t − ρ 1 Y t − 1 − . . . − ρ p Y t − p = β 0 ( 1 − ρ 1 − . . . ρ k ) + β 1 ( X t , 1 − ρ 1 X t − 1 , 1 − . . . − ρ p X t − p , 1 ) + . . . + β k ( X t , k − ρ 1 X t − 1 , k − . . . − ρ p X t − p , k ) Y_t-\rho_1Y_{t-1}-...-\rho_pY_{t-p}=\beta_0(1-\rho_1-...\rho_k)+\beta_1(X_{t,1}-\rho_1X_{t-1,1}-...-\rho_pX_{t-p,1})+...+\beta_k(X_{t,k}-\rho_1X_{t-1,k}-...-\rho_pX_{t-p,k}) Y t − ρ 1 Y t − 1 − . . . − ρ p Y t − p = β 0 ( 1 − ρ 1 − . . . ρ k ) + β 1 ( X t , 1 − ρ 1 X t − 1 , 1 − . . . − ρ p X t − p , 1 ) + . . . + β k ( X t , k − ρ 1 X t − 1 , k − . . . − ρ p X t − p , k )
OLS 估计差分模型, 得到参数无偏、有效估计量；
随机误差项相关系数估计：科克伦 - 奥科特迭代法 ：Y i = β 0 + β 1 X i + μ i Y_i=\beta_0+\beta_1X_i+\mu_i Y i = β 0 + β 1 X i + μ i o l s ols o l s e ~ t \widetilde{e}_t e t
ols 估计e ~ t = ρ 1 e ~ t − 1 + ρ 2 e ~ t − 2 + . . . + ρ p e ~ t − p + ε t \widetilde {e} _ t = \rho_1 \widetilde {e} _ {t-1} + \rho_2\widetilde {e} _ {t-2} +...+ \rho_p \widetilde {e} _ {t-p} + \varepsilon _ t e t = ρ 1 e t − 1 + ρ 2 e t − 2 + . . . + ρ p e t − p + ε t
将估计值代入广义差分模型, 进行 OLS 估计, 得到β \beta β
由参数估计值计算Y ^ i \widehat{Y}_i Y i e ~ t \widetilde{e}_t e t
一般迭代两次就可以得到较为满意的结果, 科克伦 - 奥科特两步法；
FGLS 可行的广义最小二乘法：可以求得Ω \Omega Ω
序列相关稳健标准误法：Newey-West 标准误 , 可以得到序列相关的正确标准误, 得到 OLS 正确方差估计；
虚假序列相关：
时间序列平稳可以替代随机抽样假定, 随机误差项仍满足正态分布的假定；
避免虚假回归（为回归）：
Y t = Y 0 + ∑ e 1 t Y_t=Y_0+\sum e_1t Y t = Y 0 + ∑ e 1 t
X t = X 0 + ∑ e 2 t X_t=X_0+\sum e_2t X t = X 0 + ∑ e 2 t
e 1 t e_1t e 1 t e 2 t e_2t e 2 t
显著相关关系；
平稳性：y t y_t y t
{ y 1 , y 2 , . . . , y t } \{y_1,y_2,...,y_t\} { y 1 , y 2 , . . . , y t } { y 1 + k , y 2 + k , . . . , y t + k } \{y_{1+k},y_{2+k},...,y_{t+k}\} { y 1 + k , y 2 + k , . . . , y t + k }
弱平稳性（常用）
y t y_t y t
E ( y t ) = μ E(y_t)=\mu E ( y t ) = μ
v a r ( y t ) = E ( y t − μ ) 2 = σ 2 var(y_t)=E(y_t-\mu)^2=\sigma^2 v a r ( y t ) = E ( y t − μ ) 2 = σ 2
c o v ( y t , y t + k ) = γ k = E [ ( y t − μ ) ( y t + k − μ ) ] = E [ ( y t + m − μ ) ( y t + m + k − μ ) ] cov(y_t,y_{t+k})=\gamma_{k}=E[(y_t-\mu)(y_{t+k}-\mu)]=E[(y_{t+m}-\mu)(y_{t+m+k}-\mu)] c o v ( y t , y t + k ) = γ k = E [ ( y t − μ ) ( y t + k − μ ) ] = E [ ( y t + m − μ ) ( y t + m + k − μ ) ]
非平稳时, 期望值是依赖时间变化的
常见非平稳随机过程 (stochastic processes)Y t = Y t − 1 + e t Y_t=Y_{t-1}+e_t Y t = Y t − 1 + e t
其中e t e_t e t σ 2 \sigma^2 σ 2
Y t = Y 0 + ∑ e t Y_t=Y_0+\sum e_t Y t = Y 0 + ∑ e t
then:
E ( Y t ) = E ( Y 0 + ∑ e t ) = Y 0 E(Y_t)=E(Y_0+\sum e_t)=Y_0 E ( Y t ) = E ( Y 0 + ∑ e t ) = Y 0
v a r ( Y t ) = t σ 2 var(Y_t)=t\sigma ^2 v a r ( Y t ) = t σ 2
随时间的增加, 方差会增大；
有漂浮随机游走 (Random Walk with Drift)
y t = δ + y t − 1 + e t y_t=\delta+y_{t-1}+e_t y t = δ + y t − 1 + e t δ \delta δ
X t = ϕ X t − 1 + μ t X_t=\phi X_{t-1}+\mu_t X t = ϕ X t − 1 + μ t
当− 1 < ϕ < 1 -1<\phi<1 − 1 < ϕ < 1
平稳性检验：散点图判断平稳性 （看均值或者离散程度）；样本自相关函数判断平稳性 ：
总体自相关函数(autocorrelation function, ACF)
ρ k = γ k γ 0 = c o v ( y t , y t + k ) v a r ( y t ) \rho_k=\frac{\gamma_k}{\gamma_0}=\frac{cov(y_t,y_{t+k})}{var(y_t)} ρ k = γ 0 γ k = v a r ( y t ) c o v ( y t , y t + k )
样本 ACF
ρ k ^ = γ ^ k γ ^ 0 = ∑ ( y t − y ‾ ) ( y t + k − y ‾ ) ∑ ( y t − y ‾ ) 2 \widehat {\rho_k} = \frac {\widehat {\gamma} _ k} {\widehat {\gamma} _ 0 } = \frac {\sum(y_t - \overline {y} ) (y _ {t+k}-\overline {y} ) } {\sum(y_t -\overline {y} ) ^ 2 } ρ k = γ 0 γ k = ∑ ( y t − y ) 2 ∑ ( y t − y ) ( y t + k − y )
白噪声的A C F = 0 ACF=0 A C F = 0
非平稳序列的 ACF 衰减比较慢；
White Noise (i.i.d- independent and identically distributed)σ 2 \sigma^2 σ 2
All the ACFS are zeros;
Test: Q 统计量H 0 : ρ 1 = ρ 2 = . . . = ρ k = 0 H_0:\rho_1=\rho_2=...=\rho_k=0 H 0 : ρ 1 = ρ 2 = . . . = ρ k = 0
Portmanteau (Q)Statistic：Q ∗ = T ∑ l = 1 m ρ ^ l 2 ∼ χ 2 ( m ) Q^*=T\sum^{m}_{l=1}\widehat{\rho}_l^2\thicksim\chi^2(m) Q ∗ = T ∑ l = 1 m ρ l 2 ∼ χ 2 ( m )
非平稳时间序列 ACF 特征：当 k 增大时, 衰减比较慢；
平稳时间序列 ACF 特征：当 k 增大时, 衰减比较快；
单位根 (unit root) y t = ρ y t − 1 + e t y_t=\rho y_{t-1}+e_t y t = ρ y t − 1 + e t
y t − ρ y t − 1 = e t y_t-\rho y_{t-1}=e_t y t − ρ y t − 1 = e t
y t − ρ L y t = e t y_t-\rho L y_t=e_t y t − ρ L y t = e t
( 1 − ρ L ) y t = e t (1-\rho L)y_t=e_t ( 1 − ρ L ) y t = e t
⇒ 1 − ρ z = 0 \Rightarrow 1-\rho z=0 ⇒ 1 − ρ z = 0
z = 1 ρ > 1 z=\frac{1}{\rho}>1 z = ρ 1 > 1
ρ = 1 \rho=1 ρ = 1
∣ ρ ∣ < 1 |\rho|<1 ∣ ρ ∣ < 1 y t y_t y t
若y t = 2 y t − 1 − y t − 2 + e t y_t=2y_{t-1}-y_{t-2}+e_t y t = 2 y t − 1 − y t − 2 + e t z 1 = 1 , z 2 = 1 z_1=1, z_2=1 z 1 = 1 , z 2 = 1
Dickey-Fuller 单位根检验
y t = ρ y t − 1 + e t y_t=\rho y_{t-1}+e_t y t = ρ y t − 1 + e t
两边同时减去y t − 1 y_{t-1} y t − 1
then:y t − y t − 1 = ( ρ − 1 ) y t − 1 + e t y_t-y_{t-1}=(\rho-1)y_{t-1}+e_t y t − y t − 1 = ( ρ − 1 ) y t − 1 + e t Δ y t = δ y t − 1 + e t \Delta y_t=\delta y_{t-1}+e_t Δ y t = δ y t − 1 + e t
检验原假设：H 0 : δ = 0 H_0:\delta=0 H 0 : δ = 0
Augmented Dickey-Fuller (ADF) test
Δ y t = δ y t − 1 + ∑ j = 1 L λ j Δ y t − j + e t \Delta y_t = \delta y _ {t-1} + \sum ^ {L} _ {j=1} \lambda_j \Delta y _ {t-j} + e_t Δ y t = δ y t − 1 + ∑ j = 1 L λ j Δ y t − j + e t
Δ y t = α + δ y t − 1 + ∑ j = 1 L λ j Δ y t − j + e t \Delta y_t = \alpha+\delta y_ {t-1}+\sum^{L} _ {j=1} \lambda_j \Delta y_{t-j}+ e_t Δ y t = α + δ y t − 1 + ∑ j = 1 L λ j Δ y t − j + e t
Δ y t = α + β t + δ y t − 1 + ∑ j = 1 L λ j Δ y t − j + e t \Delta y_t=\alpha+\beta t+\delta y_{t-1} + \sum^{L} _ {j=1} \lambda_j \Delta y_{t-j} + e_t Δ y t = α + β t + δ y t − 1 + ∑ j = 1 L λ j Δ y t − j + e t
带有时间趋势项的非平稳序列, 可以通过去除趋势项使其变的平稳；
针对H 0 : δ = 0 H_0:\delta=0 H 0 : δ = 0
模型 3-2-1 的顺序进行检验
单整序列：I ( 1 ) I(1) I ( 1 )
变量之间存在长期稳定的关系, 即变量之间协整, 可以使用经典回归模型方法建立回归模型；
经济变量之间长期均衡：Y t = α 0 + α 1 X t + μ t Y_t=\alpha_0+\alpha_1X_t+\mu_t Y t = α 0 + α 1 X t + μ t μ t = Y t − α 0 − α 1 X t \mu_t=Y_t-\alpha_0-\alpha_1X_t μ t = Y t − α 0 − α 1 X t
协整：Y t , X t ∼ C I ( 1 , 1 ) Y_t,X_t\thicksim CI(1,1) Y t , X t ∼ C I ( 1 , 1 )
协整检验：EG 检验 Y t = α 0 + α 1 X t + μ t Y_t=\alpha_0+\alpha_1X_t+\mu_t Y t = α 0 + α 1 X t + μ t e ^ t \widehat{e}_t e t
多变量协整检验
高阶单整变量的协整检验
只能有协整检验均衡：
误差修正：Δ Y t = α 1 Δ X t + v t \Delta Y_t=\alpha_1\Delta X_t+v_t Δ Y t = α 1 Δ X t + v t
v t v_t v t
采用差分形式估计, 关于变量水平值的重要信息将被忽略, 只表达了 X 与 Y 之间的短期关系, 没有揭示长期关系；
Y 在 t 期的变化, 不仅取决于 X 本身的变化, 还取决于 X 与 Y 在 t-1 期末的状态；
误差修正模型：（ECM 模型 -DHSY 模型）Y t = α 0 + α 1 X t + μ t Y_t=\alpha_0+\alpha_1X_t+\mu_t Y t = α 0 + α 1 X t + μ t Y t = β 0 + β 1 X t + β 2 X t − 1 + β 3 Y t − 1 + μ t Y_t=\beta_0+\beta_1X_t+\beta_2X_{t-1}+\beta_3Y_{t-1}+\mu_t Y t = β 0 + β 1 X t + β 2 X t − 1 + β 3 Y t − 1 + μ t Δ Y t = β 1 Δ X t − ( 1 − β 3 ) ( Y t − 1 − β 0 1 − β 3 − β 1 + β 2 1 − β 3 ) + μ t \Delta Y_t= \beta_1\Delta X_t-(1-\beta_3)(Y_{t-1}-\frac{\beta_0}{1-\beta_3}-\frac{\beta_1+\beta_2}{1-\beta_3})+\mu_t Δ Y t = β 1 Δ X t − ( 1 − β 3 ) ( Y t − 1 − 1 − β 3 β 0 − 1 − β 3 β 1 + β 2 ) + μ t Δ Y t = β 1 Δ X t − λ ( Y t − 1 − α 0 − α 1 X t − 1 ) + μ t \Delta Y_t= \beta_1\Delta X_t-\lambda(Y_{t-1}-\alpha_0-\alpha_1X_{t-1})+\mu_t Δ Y t = β 1 Δ X t − λ ( Y t − 1 − α 0 − α 1 X t − 1 ) + μ t Y Y Y X X X Δ Y t = β 1 Δ X t − λ e c m t − 1 + μ t \Delta Y_t= \beta_1\Delta X_t-\lambda ecm_{t-1}+\mu_t Δ Y t = β 1 Δ X t − λ e c m t − 1 + μ t α 0 + α 1 X t \alpha_0+\alpha_1X_t α 0 + α 1 X t α 1 \alpha_1 α 1 Y t = β 0 + β 1 X t + β 2 X t − 1 + β 3 Y t − 1 + μ t Y_t=\beta_0+\beta_1X_t+\beta_2X_{t-1}+\beta_3Y_{t-1}+\mu_t Y t = β 0 + β 1 X t + β 2 X t − 1 + β 3 Y t − 1 + μ t β 1 \beta_1 β 1
误差修正：引入更多滞后项Δ Y t − 1 \Delta Y_{t-1} Δ Y t − 1 Δ X t − 1 \Delta X_{t-1} Δ X t − 1
误差修正：多变量
建立误差修正模型：EG 两步法 ：OLS 协整回归, 将 OLS 估计的非均衡误差项的滞后一期加入回归, 估计短期弹性；
Δ Y t = l a g g e d ( Δ Y t , Δ X t ) − λ e c m t − 1 + μ t \Delta Y_t=lagged(\Delta Y_t,\Delta X_t)-\lambda ecm_{t-1}+\mu_t Δ Y t = l a g g e d ( Δ Y t , Δ X t ) − λ e c m t − 1 + μ t
直接估计法 ：对Δ Y t = λ α 0 + β Δ X t − λ Y t − 1 + λ α 1 X t − 1 + μ t \Delta Y_t=\lambda \alpha_0+\beta \Delta X_t-\lambda Y_{t-1}+\lambda \alpha_1X_{t-1}+\mu_t Δ Y t = λ α 0 + β Δ X t − λ Y t − 1 + λ α 1 X t − 1 + μ t
随机时间序列模型：不同时点观测值之间的关系；
序列自回归模型：
A R ( p ) : X t = ϕ 1 X t − 1 + . . . + ϕ p X t − p + μ t AR(p):X_t=\phi_1X_{t-1}+...+\phi_pX_{t-p}+\mu_t A R ( p ) : X t = ϕ 1 X t − 1 + . . . + ϕ p X t − p + μ t
MA(q):μ t = ε t − θ 1 ε t − 1 − . . . − θ q ε t − q \mu_t=\varepsilon_t-\theta_1\varepsilon_{t-1}-...-\theta_q\varepsilon_{t-q} μ t = ε t − θ 1 ε t − 1 − . . . − θ q ε t − q
ARMA(p, q):X t = ϕ 1 X t − 1 + . . . + ϕ p X t − p + ε t − θ 1 ε t − 1 − . . . − θ q ε t − q X_t=\phi_1X_{t-1}+...+\phi_pX_{t-p}+\varepsilon_t-\theta_1\varepsilon_{t-1}-...-\theta_q\varepsilon_{t-q} X t = ϕ 1 X t − 1 + . . . + ϕ p X t − p + ε t − θ 1 ε t − 1 − . . . − θ q ε t − q
可使用过去的行为预测未来
AR(p)模型的平稳性X t − ϕ 1 X t − 1 − . . . − ϕ p X t − p = ε t X_t-\phi_1X_{t-1}-...-\phi_pX_{t-p}=\varepsilon_t X t − ϕ 1 X t − 1 − . . . − ϕ p X t − p = ε t
( 1 − ϕ 1 L 1 − . . . − ϕ p L p ) X t = ε t (1-\phi_1 L^1-...-\phi_pL^p)X_t=\varepsilon_t ( 1 − ϕ 1 L 1 − . . . − ϕ p L p ) X t = ε t
得到 AR(p)的特征方程ϕ ( z ) = ( 1 − ϕ 1 z 1 − . . . − ϕ p z p ) = 0 \phi(z)=(1-\phi_1 z^1-...-\phi_p z^p)=0 ϕ ( z ) = ( 1 − ϕ 1 z 1 − . . . − ϕ p z p ) = 0
所有根 z 的模大于 1, 则是平稳的；
高阶自回归平稳性充分条件：∣ ϕ 1 ∣ + . . . + ∣ ϕ p ∣ < 1 |\phi_1|+...+|\phi_p|<1 ∣ ϕ 1 ∣ + . . . + ∣ ϕ p ∣ < 1
MA(q)的平稳性：
ARMA(p, q)的平稳性取决与 AR(p)部分的平稳性
由 ACF 及 PACF 判断模型类别：拖尾 / 截尾
向量自回归：
格兰杰因果检验：Y t Y_t Y t R S S U RSS_U R S S U Y t Y_t Y t R S S R RSS_R R S S R = R S S R − R S S U / m R S S U / ( n − k ) ∼ F α ( m , n − k ) =\frac{RSS_R-RSS_U/m}{RSS_U/(n-k)}\thicksim F_{\alpha}(m,n-k) = R S S U / ( n − k ) R S S R − R S S U / m ∼ F α ( m , n − k )
